Związkiem statystycznym (korelacją) jest związek jednej cechy ze średnią wartością drugiej (program uprawnienia budowlane). Analiza korelacyjna jest działem statystyki, która zajmuje się metodami określania podobnych związków. Podczas stosowania analizy korelacyjnej ważny jest rodzaj oraz ścisłość korelacji. Rodzaj korelacji można określić dzięki liczbie i przebiegu zmian cech poddanych analizie.

Korelacją jednokrotną jest związek statystyczny dwóch cech. Korelacja liniowa ma miejsce w sytuacji proporcjonalności zmian analizowanych cech. Z kolei w sytuacji, kiedy nie ma proporcjonalności, korelacja nosi nazwę krzywoliniowej. Korelacja wielokrotna ma miejsce w przypadku związku statystycznego powyżej dwóch cech (egzamin na uprawnienia budowlane).

Ścisłość korelacji można określić stopniem wzajemnego powiązania analizowanych własności, które zależą od ich wariacji. W sytuacji, kiedy każdej wartości jednej cechy odpowiadają wartości drugiej i jednocześnie są one bliskie średniej, to korelacja nosi nazwę ścisłej. Granicznym przypadkiem największej ścisłości jest oczywiście związek funkcyjny. Ścisłość korelacji jest mała, kiedy wartości cechy są silnie rozproszone wokół pewnej średniej wartości. W drugim przypadku granicznym może wystąpić brak jakiejkolwiek korelacji. Miarą liczbową ścisłości są: współczynnik korelacji, stosunek korelacyjny i inne charakterystyki.

Statystyczne określenie związku dwóch zmiennych

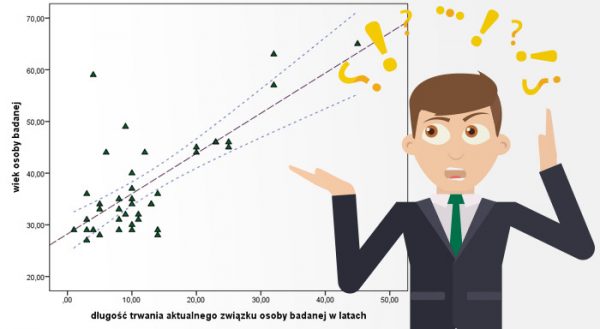
Żeby udało się określić statystyczny związek dwóch zmiennych y oraz x, konieczne jest to, aby przeprowadzić w pierwszej kolejności szereg pomiarów doświadczalnych tych wartości. Kolejnym krokiem jest zastosowanie analizy korelacyjnej. Zanim dojdzie się do właściwej analizy, należy zestawić ze sobą wyniki pomiarów w wyjściowej tablicy korelacyjnej. Na przecięciu się każdej kolumny i wiersza wyjściowej tablicy korelacyjnej, znajduje się częstość mxy. Częstość ta wskazuje na to, ile razy przy dowolnych wartościach x otrzymano określoną wartość y (program jednolite akty prawne na egzamin uprawnienia).

Z uwagi na to, że dolna graniczna wartość r jest całkiem bliska wartości 1, można śmiało stwierdzić, że istnieje korelacja analizowanych wielkości y i x. Są to wielkości, które określają prędkość rozchodzenia się fal ultradźwiękowych w betonie i jego wytrzymałości na ściskanie. Dodatkowo należy mieć na uwadze, że analiza korelacyjna prowadzi zawsze do dwu nieodwracalnych równań regresji. Nie jest to przeszkodą z uwagi na charakter analizy, która ma na celu poglądowe zbadanie istnienia ogólnego związku V i R.

Zdarza się tak, że w pewnych opracowaniach dąży się do tego, żeby otrzymać uogólnione równania. Dzięki temu można określić y przy znanym x oraz odwrotnie (program na uprawnienia budowlane w wersji android). Zanim określi się parametry równania krzywej regresji, konieczne jest, żeby przeprowadzić analizę, która pozwoli na to, żeby dobrać ). Jest to możliwe do uzyskania wyłącznie w sytuacji, kiedy r jest bliskie 1. Prowadzi się wówczas prostą, która jest dwusieczną kąta, który powstał dzięki dwóm prostym regresji. Prostą tę najczęściej uważa się za pewnego rodzaju przeciętną prostą regresji. Jednocześnie nie ma to żadnego uzasadnienia w matematyce.

W sytuacji, kiedy współczynnik korelacji jest mały, czyli dużo mniejszy od 1, możliwy jest korelacyjny związek krzywoliniowy. To, że współczynnik ten jest mniejszy od 1, oznacza, że nie ma korelacji liniowej. Zanim określi się parametry równania krzywej regresji, konieczne jest, żeby przeprowadzić analizę, która pozwoli na to, żeby dobrać krzywą, która jest jak najbardziej zbliżona do wyników doświadczalnych, które przedstawia się na wykresie.